BASIC STATISTICS FOR DATA SCIENTISTS PART 2
April 28, 2019
One Sample Tests
One sample tests help us test hypotheses regarding whether a population parameter is equal to (or less than/more than) a specific value.
We do not use one sample tests becasue as you can see from the examples above, they do not help answer interesting questions for us. Unless we have a reason to believe why a certain population parameter should be a certain value, one sample tests are uninteresting. The interesting questions are whether the difference between two populations (one exposed to a product change and one not exposed to the product change) are significantly different than 0 or not. Such questions can be answered by two-sample tests but we will cover one sample tests first to build up the theory slowly.
Definitions
Null Hypothesis: This is the hypothesis we want to reject. So we assume this is true and then gather evidence against it to be able to reject it. If the evidence against the null at the end of an experiment is strong enough, by a measure of strength to be defined soon, we reject the null hypothesis.
Alternative Hypothesis: Alternative hypothesis is the negation of the null hypothesis. The union of the two should always cover all potential parameter values.
One-sided vs Two-sided tests: Tests whose null hypothesis are posed in the form of ‘parameter is less than/greater than a certain value’ are called one-sided tests while those whose null hypothesis is posed in the form of ‘parameter is equal to a certian value’ are called two-sided tests. All comparative tests (‘regular AB’), are two sample two sided tests. They test whether the difference between two populations is 0 or not. If the difference observed is too far away from 0 in either direction (improvement or hurting) we reject and can conclude the treatment is hurtful or benefitial. On the other hand, the non-inferiority test is a one-sided test. It tests whether the difference between two populations is less than the non-inferiority threshold or not. If we reject the null, we can conclude that the difference is not less than our allowed cost but we can never make a claim for results that are in the other direction.
Test-statistic: The test statistic is the standardized quantity of the observed statistic coming from the experiment. Put other way, the test statistic tells us how many standard deviations the observed statistic is away from the hypothesized mean. For example, if the statistic we collect is the sample mean, then the test statistic is the standardized observed mean. The test-statistic allows us to see where on the standardized sampling distribution our observation falls. Standardization allows us to communicate how extreme the observed quantity is regardless of the context (read units).
p-value: The p-value of a test is what quantifies the ‘strength’ of the evidence against the null. P-value is the probability that we would get a result that is as extreme or more as the one we observed if the null hypothesis is true. It translates to the area beyond the test statistic under the standardized sampling distribution.
Critical Point and Rejection Region: The critical point is the point on the standardized sampling distribution beyond which we would reject the null hypothesis. Where this point lies depends on the false positive rate referred as \(\alpha\). In ET, we use \(\alpha = 0.10\) for comparative tests and an \(\alpha\) value of $0.10The area beyond the critical point is sometimes referred as the rejection region.
One Sample Test for the Mean
Let’s put all the definitions above to use with an example of a one-sample test for the mean.
Consider the case where we want to know whether the mean page load time is greater than 2 miliseconds.
\[ H_{0}: \mu <= 2 \text{ms} \] \[ H_{1}: \mu > 2 \text{ms} \] Let’s say for arguments sake we have access to the entire population and the population has a mean of 2.4ms pageload time that is coming from an exponential distribution (to make the point that a normally distributed population is not required).
set.seed(7)
N <- 100000
pop <- rexp(N, 1/2.4)
mu <- mean(pop)
sigma <- sqrt(var(pop)*(N-1)/N)
hist(pop)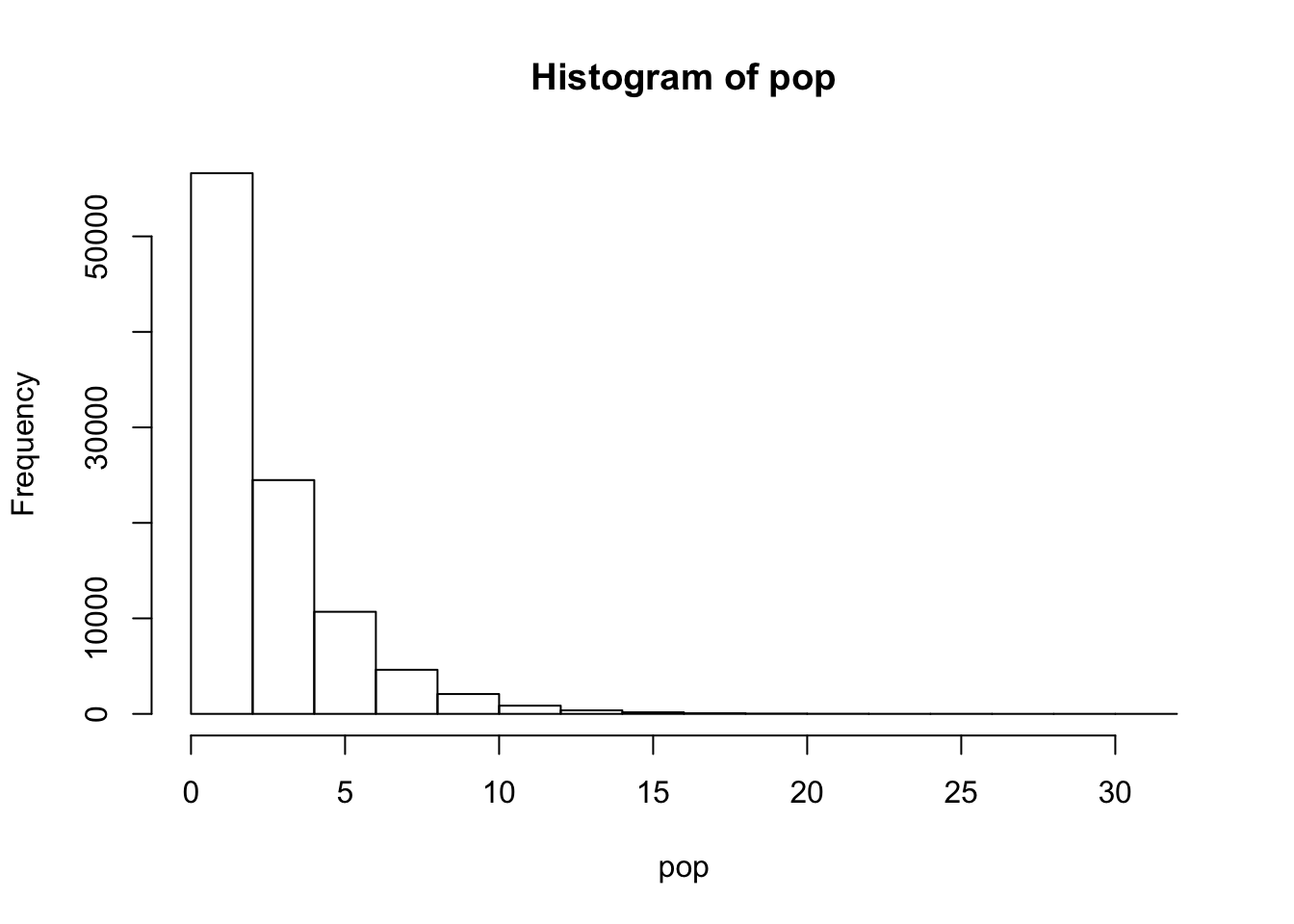
n <- 1000
samp <- sample(x = pop,size = n, replace = FALSE)
x_bar <- mean(samp)
sigma_hat <- sqrt(var(samp))
se <- sqrt((sigma_hat^2)/n)
t.test(samp, mu = 2, alternative = 'greater')##
## One Sample t-test
##
## data: samp
## t = 3.2782, df = 999, p-value = 0.0005403
## alternative hypothesis: true mean is greater than 2
## 95 percent confidence interval:
## 2.121613 Inf
## sample estimates:
## mean of x
## 2.244309Let’s put all the things we covered in previous chapter to use.
Assuming the null hypothesis is correct, the mean of the sampling distribution will be centered at the true mean which is 2ms. The standard deviation of the sampling distribution (standard error from now on) will be the true population variance divided by the sample size (\(\sigma^{2}/N)\)), and therefore
\(\frac{\bar{X} - \mu}{\sqrt{\sigma^{2}/N}} \sim N(0,1)\). However, note that to leverage this information, we need to know the true population variance \(\sigma^{2}\). If we use our sample to estimate this parameter \(\hat{\sigma}^{2}\) theory tell us \(\frac{\bar{X} - \mu}{\sqrt{\hat{\sigma}^{2}/N}} \sim T(0,df=N-1)\).
Then, if the null is true,
\(\frac{\bar{X} - \mu}{\sqrt{\hat{\sigma}^{2}/N}} \sim T(0,df=N-1)\)
which means, if \(H_{0}\) is true 3.2782255 is a draw from \(T(0,df=1000-1)\)
the critical value is 1.6463803. Since our test statistic is greater than the critical value, meaning what we observed is more extreme than what we subjectively allow to be attributable to chance (5%), we will reject the null and conclude that the average pageload time is greater than 2ms.
One Sample Test for Proportions
In this example, we will compare proportions intead of means of continuos variables.
Consider the case where we want to know whether the conversion on a certain page for a certain metric is 0.5 or not.
\[ H_{0}: \pi = 0.5 \] \[ H_{1}: \pi \neq 0.5 \]
set.seed(7)
N <- 100000
pop <- rbinom(n = N, size = 1, p = 0.5)
pi <- mean(pop)
sigma <- sqrt(var(pop)*(N-1)/N)
sigma2 <- sqrt(pi*(1-pi))
hist(pop)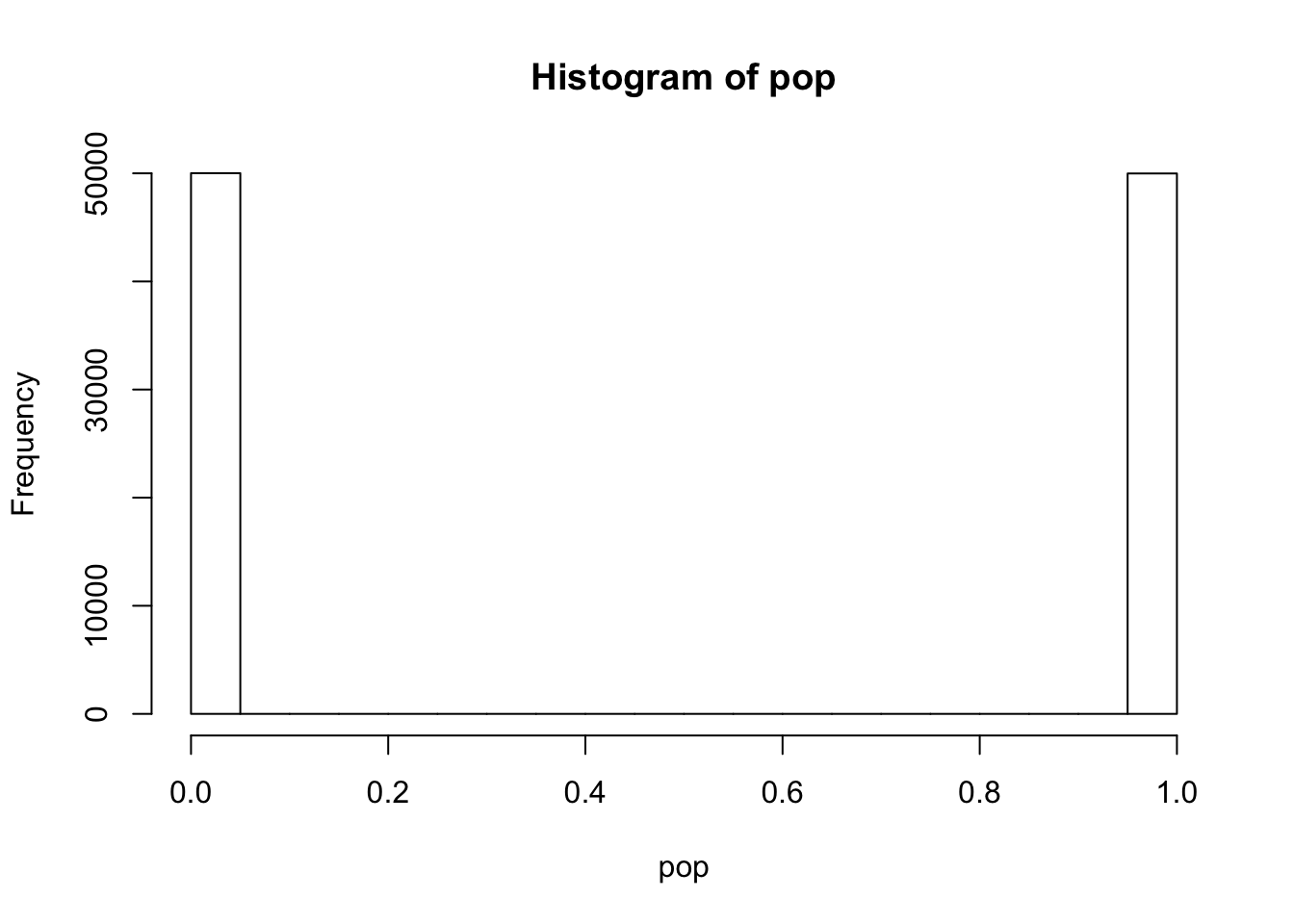
n <- 1000
samp <- sample(x = pop,size = n, replace = FALSE)
p <- mean(samp)If the null hypothesis is correct, we know that
\[ \frac{p - \pi}{\sqrt{\sigma^{2}/N}} \sim N(0,1) \] The difference of proportions from means is that we do not need to estimate \(\sigma\) because there is a direct relationship between mean and variance for a binomial distribution. That is,
\[ \sigma^{2} = \pi * (1- \pi) \]. So, \[ \frac{p - \pi}{\sqrt{\pi (1-\pi)/N}} \sim N(0,1) \]
This is so, as long as the distribution of proportion can be approximated with a normal distribution. But we know normal approximation for a binomial distribution is a good one so long as the sample size is not too small.
Then under \(H_{0}\), we expect 1.2649111 to be N(0,1).
So, our observed proportion is 1.2649111 standard deviation away from zero. We will reject the null if the observed proportion is at least 1.6448536 standard deviations away from zero. Since 1.2649111 isn’t greater than 1.6448536 we fail to reject the null hypothesis.
The p-value is 1.7940968 which is not less than 0.05, another way of looking at whether the result is significant or not.
the test we have conducted above is known as a one sample z-test.
The G-Test, The Chi-Squared Test and Their Connection to the z-test in ET
You may have heard that AB tests use a G-test for binary metrics and not the z-test. Is there a difference? Let us start with a Chi Squared test. We will show that for a binary metric, a z-test and a Chi-Squared test are equavalent and then make the connection between the chi squared test and the G test. Again most AB test platforms use the G-test to test binary metrics.
We can represent our data as total number of 1s and 0s (1 = converted, 0 = did not convert).
If the null is correct and \(\pi = 0.5\), then we expect 500 converters and 500 non converters.
library(knitr)
library(tidyverse)## ── Attaching packages ──────────────────────────────────────────────────────────────────────────────────────────────────────── tidyverse 1.2.1 ──## ✔ ggplot2 3.1.0 ✔ purrr 0.2.5
## ✔ tibble 2.0.0 ✔ dplyr 0.7.8
## ✔ tidyr 0.8.2 ✔ stringr 1.3.1
## ✔ readr 1.3.1 ✔ forcats 0.3.0## ── Conflicts ─────────────────────────────────────────────────────────────────────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::lag() masks stats::lag()summ <- as.tibble(table(samp))## Warning: `as.tibble()` is deprecated, use `as_tibble()` (but mind the new semantics).
## This warning is displayed once per session.summ <- summ %>%
transmute(Cell = samp,
Observed = n) %>%
mutate(Expected = c(500,500))
kable(summ)| Cell | Observed | Expected |
|---|---|---|
| 0 | 480 | 500 |
| 1 | 520 | 500 |
The chi squared goodness of fit test then says:
\[ \sum_{i=1}^{C} \frac{(O_{i}-E_{i})^2}{E_{i}} \sim \chi_{k} \]
where i is an index for cells, N is the total number of cells and k is the degrees of freedom for the chi squared distribution.
In a binary metric case, C = 2, and k = C - 1 = 1.
If the hypothesized proportion of map bookers is \(\pi\) and observed proportion is \(p\) realize
\[O_{1} = Np \text{ and } O_{2} = N - Np = N (1-p)\] \[E_{1} = N \pi \text{ and } E_{2} = N - N \pi = N(1-\pi)\] Plugging the above into the test statistic we get:
\[ \frac{(Np - N \pi)^{2}}{N \pi} + \frac{\bigg(N\big((1-p)-(1-\pi)\big)\bigg)^2}{N(1-\pi)}\]
A little algebra gets us:
\[ \bigg(\frac{(p - \pi)}{\sqrt{(\pi(1-\pi)/N)}}\bigg)^{2} \]
Observe the test statistic for the chi-square test for a binomial metric is the test statistic we used in the z test raised to second power. So we expect it to be distributed as the square of a standard normal. And a chi-square distribution with one degree of freedom is defined to be the square of a standard normal.
So testing the square of the test ststistic using a chi square distribution with 1 degree of freedom is equivalant to testing the test statistic using a standard normal.
To see this real quick, if we look at the p-value for the chi-square test we will see where on a chi-square (df=1) distribution the test statistic squared falls. 0.2059032. Realize we get the same p-value as the z-test.
Okay now that we have established the equavalance between the z and chi square tests for binary metrics, let’s finally go over the G-test.
G-test is what is known a likelihood ratio test. The test statistic is
\[ G = 2 \sum_{i=1}^{C}O_{i} \text{ ln}\big(\frac{O_{i}}{E_{i}}\big) \] G is approximately distributed as a chi-square with C - 1 degrees of freedom like the chi-square test statistic. Asymptotically G like Chi square test statistic is chi-square distributed.
Confidence Intervals and p-value CI duality
What is a confidence interval?
In AB tests, not only the p-value is reported but also a confidence interval around a point estimate. Let’s quickly define a confidence interval and show how to calculate it and then we can talk about the connection between p-values and confidence intervals.
Confidence Interval: In the frequentist framework, we treat population parameters as fixed values. There is a true population mean, there is a true population proportion. These values do not vary. What varies is the sample we take from the population and thus the sample statistics (sample mean, sample proportion). The sample statistics are our ‘best’ guess for the population parameter but there is uncertainty in this guess due to the random nature of the sample.
To account for this variation we build confidence intervals and report the intervals along with the point estimates. A 95% confidence interval around our sample mean for example means that the sample we picked from the population has a 95 per cent probability to contain the true population parameter.
A nice way of seeing this is as follows: Just like the sampling distribution, imagine all the possible samples we could draw from the population for a fixed sample size. If we build confidence intervals around the point estimates for each of these sample estimates and then put those confidence intervals in a bag and then pick one confidence interval from this bag, we have a 95% chance of picking an interval from this bag that will contain the true population parameter.
The trick is to avoid statements that would sound like the population parameter is random. Any statement that sounds like the population parameter is random is a wrong interpretation of a CI. What is random is the sample!
How to calculate a confidence interval?
The formula for an \(\alpha\) confidence interval is
\[ \text{sample_statistic } \pm \text{ standard_error} * t_{1-\alpha/2} \]
if we are building the CI for a z-test then we shold replace the $ t_{1-/2} $ with $ z_{1-/2} $.
The intuition behind this formula is striaght forward. We by now know that the sample statistic comes from (a draw from) the sampling distribution whose standard deviation is the standard error. If the true value of the parameter is the sample statistic we observed we know the sampling distribution is centered around the sample statistic. We want to cover as much area as our confidence interval. The standardized score tells us exactly the point that covers that much area on the standardized distribution. By multiplying with the standard error we know that point in the units of the parameter so we can add and substract that from our estimate.
What is the connection between the CI and the p-value?
There is a duality between a confidence interval and hypothesis testing/p-values.
You already make use of this fact if you ever look whether 0 is outside the confidence bounds in a comparative test or if the acceptable cost is below the lower bound of the confidence interval in a non-inferioirty test to check the significance of these tests.
You can always do this because the p-value being smaller than your alpha level always correspond to the bounds of the confidence interval not including the parameter values specified in the null hypothesis.
Let’s quickly show this in a one sided test for means case. You can follow the calculatons to extend it to two sided cases easily.
Revisiting our first example with the pageload times:
\[ H_{0}: \mu <= 2 \text{ms} \] \[ H_{1}: \mu > 2 \text{ms} \]
We reject the null hypothesis if the p-value is less than 0.05. That means if the probability of observing a sample mean as big as ours or bigger given the true mean is 2ms is 0.05 or less, we will reject. Matehmatically
\[ P\bigg(\frac{\bar{X} - 2}{\text{standard errer}} > z_{0.95}\bigg)< 0.05\] We will reject the null.
so
\[ P(\bar{X}- \text{standard errer}* z_{0.95} > 2) < 0.05\] We will reject the null.
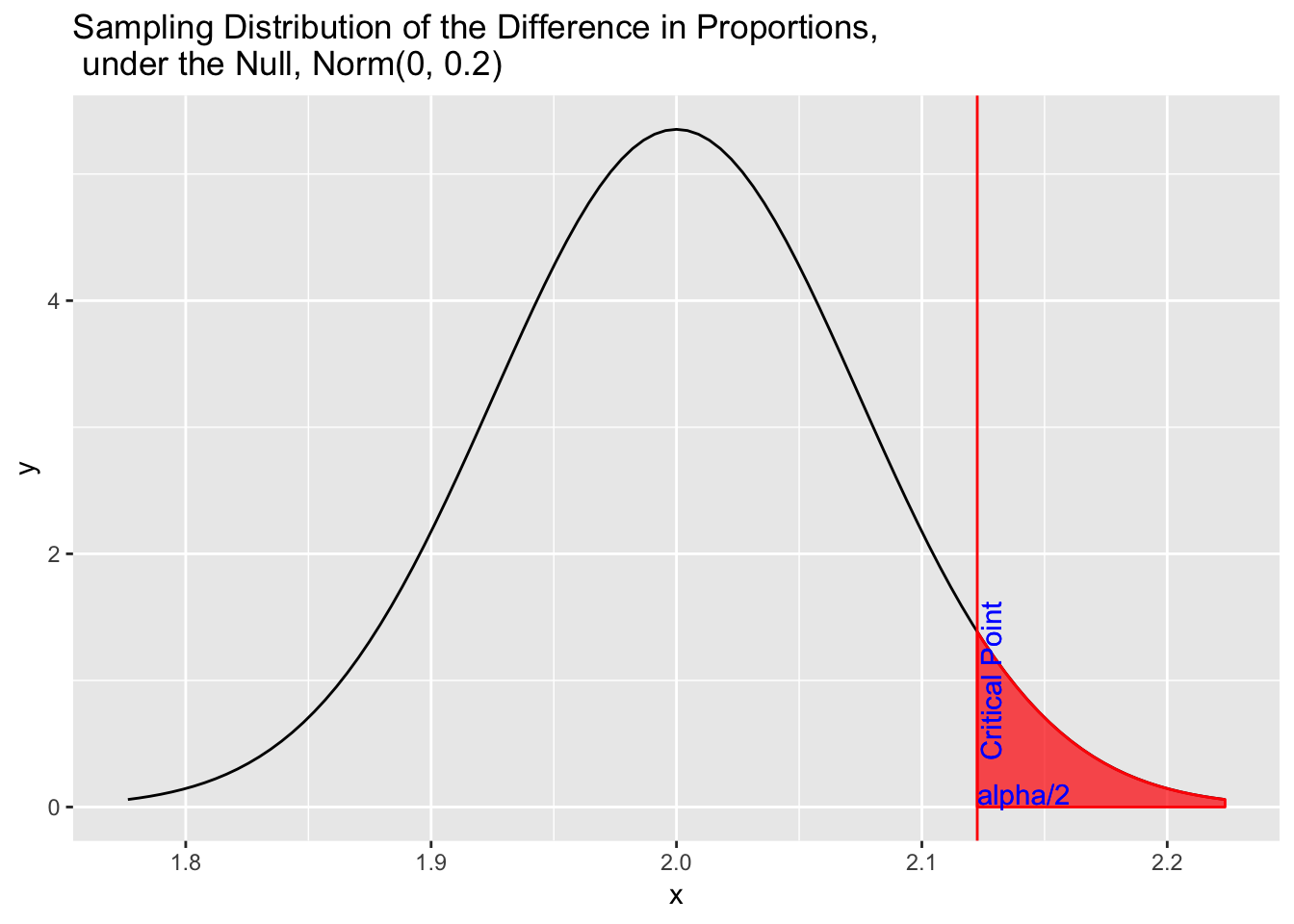
Realize the left hand side of the inequality is the lower bound of this one sided test (for one sided tests the upper bound is infinity). So this means, if the test is significant, the lower bound of the confidence interval is above the hypothesized null parameter value (with less than 5% probability that is). This is exactlt how we construct the confidence intervals too.
library(ggplot2)
p <- ggplot(data.frame(x = c(2 - 0.07452485*3, 2 + 0.07452485*3)), aes(x)) +
stat_function(fun = dnorm, args = list(mean = 2, sd = 0.07452485)) +
stat_function(fun = dnorm, args = list(mean = 2, sd = 0.07452485), xlim = c(qnorm(.1/2,2,0.07452485,FALSE), 2 + 0.07452485*3), geom = "area", fill='red', color='red', alpha = 0.7)
p + geom_vline(xintercept=qnorm(.1/2,2,0.07452485,FALSE), color='red') +
geom_text(aes(x=qnorm(.1/2,2,0.07452485,FALSE), label="Critical Point", y=1), colour="blue", angle=90, vjust = 1.2) +
geom_text(aes(x=qnorm(.1/2,2,0.07452485,FALSE), label="alpha/2", y=0.1), colour="blue", hjust = 0, angle=0) +
ggtitle("Sampling Distribution of the Difference in Proportions, \n under the Null, Norm(0, 0.2)")